Prompt Engineeringのテクニック、"Tree of Thoughts"について調べてみました。

こんにちは、CCCMKホールディングスTECH LABの三浦です。

学生の頃に好きだった漫画を久しぶりに読みました。数十年ぶりに読んだのですが、当時何度も繰り返し読んだストーリーなのでしっかり今でも内容を覚えていました。当時と違って今はインターネットで色々な考察している人たちの意見を見ることが出来ます。このシーンってこういう意味だったんだ！と今になって新しい角度からストーリーを見ることが出来たりして、結構楽しいです。昔読んだ漫画や小説を、今もう一度読み返してみるのって面白いな、と感じました。

さて、今回はPrompt Engineeringのテクニックの一つ、"Tree of Thoughts"について取り上げてみたいと思います。このテクニックは一定の粒度で分割された思考ステップを評価しながら選択していき、最終的には多様で複雑な思考プロセスを構築させることでより複雑なタスクをLLMsに解かせることを可能にします。

実際に試してみたいな、と思ったのですが、一度提案論文を調べておきたいと思い、今回以下の論文を参照しながらTree of Thoughtsについてまとめてみました。

Title: Tree of Thoughts: Deliberate Problem Solving with Large Language Models
Authors: Shunyu Yao, Dian Yu, Jeffrey Zhao, Izhak Shafran, Thomas L. Griffiths, Yuan Cao, Karthik Narasimhan
Submitted: 17 May 2023
Arxiv URL: https://arxiv.org/abs/2305.10601

Tree of Thoughts

まずTree of Thoughts以前に提案されているテクニックとTree of Thoughtsの違いを見ていきます。

一番ベーシックなテクニックはˤ"Input-Output Prompting(IO)"です。指示部分といくつかの例示を含むPromptにタスクへの入力を組み込んでLLMsに与え、タスクへの回答を生成させるテクニックです。回答に至るまでに何ステップも踏まなければいけない複雑なタスクの場合だと、このテクニックでは対処しきれない場合が出てきます。

そこで"Chain-of-Thought(CoT)"というテクニックが提案されました。これはLLMsに回答に至るまでに必要になるステップを生成させ、そのステップを連続して実行していく(Chain)ことで回答にたどり着かせることを可能にするテクニックです。たとえば数学に関連する問題だと、数式を解くためにはいくつかの式変形を繰り返して回答にたどり着くことになります。CoTを使うことで、LLMsに回答に至るまでにいくつものステップが必要であることを認識させ、実行させることが可能になります。

CoTはステップのどこかに誤りがあると、それを補正できないまま最後の回答も間違ってしまう、ということがあります。そこでステップで構成される一連のプロセスを複数回独立して実行し、それらの結果を集計してもっとも多く得られた回答を最終的な回答にする、といった方法を取ることで、より安定した回答を得られるようにしよう、というテクニックが提案されました。これが"Self-consistency with CoT(Cot-SC)"というテクニックです。

Cot-SCは複数のプロセスが実行されるものの、それぞれのプロセスは完全に独立し、かつ一方向です。たとえばプロセスの途中で、いくつもの選択肢の中からどの思考を選ぶべきか、といった考察を行うことは出来ないし、誤りに気付いて戻ることも出来ません。

そこで今回のテーマである"Tree-of-Thoughts(ToT)"では問題解決までのプロセスを複数のステップに分割し、現在時点から見てより最適なステップを選択しながらプロセスを構築していきます。もしどのステップを選択してもタスクを解決出来ない場合、ひとつ前の状態に戻ってステップを選択しなおすことも可能です。現時点で考えられるステップの生成も、LLMs自身が都度行います。ステップを選択しながら現在から次の状態に遷移していく流れは木構造を構成します。

Cot, Cot-SC, そしてToTの流れを表現した図を論文から転載します。

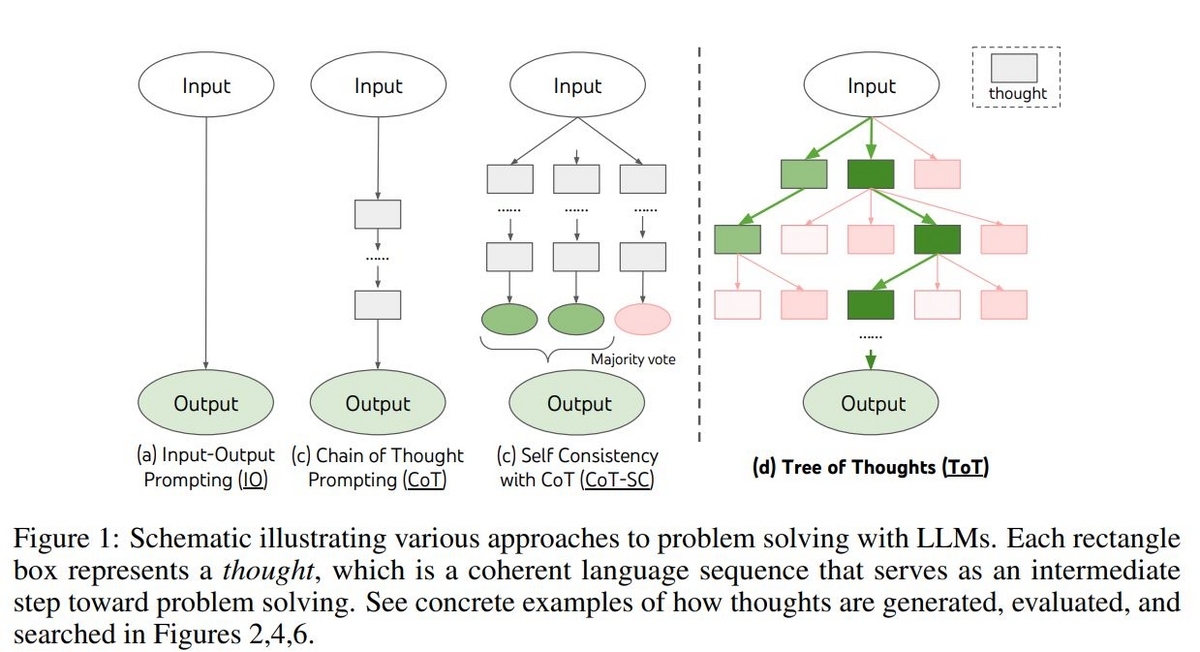
Tree of Thoughts: Deliberate Problem Solving with Large Language Models, Shunyu Yao, Dian Yu, Jeffrey Zhao, Izhak Shafran, Thomas L. Griffiths, Yuan Cao, Karthik Narasimhan, Figure 1

ToTの仕組み

ここからはもう少し詳しくToTについてまとめていきます。ToTを実装するためにはToTを構成する4つの要素を実装していく必要があります。

選択する思考ステップ

まずは選択する思考ステップをどのような形式にするのかをデザインする必要があります。たとえば数学の問題だったら次に解くべき1行の数式などです。思考ステップは大きすぎるとプロセスの中で選択できる思考ステップが少なくなり、プロセスの多様性が失われてしまいますし、逆に小さすぎると最適な思考ステップの評価が難しくなってしまいます。

現状から考えられる次に取るべき思考ステップの生成

今の状態から、次に選ぶべき思考ステップを複数個生成する関数を考える必要があります。この関数は内部ではLLMsを使用します。使用するLLMsを $p_{\theta}$ , タスクに対する入力 $x$ とこれまでの思考ステップ $z_1...z_i$ で表現した現在の状態 $s=[x, z_{1},..,z_{i}$ ]、および生成したい次の思考ステップの数 $k$ とした場合、この関数は $G(p_{\theta}, s, k)$ と表現することが出来ます。

状態の評価関数を定義する

思考ステップを選択することで遷移する次の状態を評価する関数を定義する必要があります。この評価関数を用いてToTではタスクの解決に至るまでのプロセスを木構造から探索します。この関数も内部でLLMsを使用します。使用するLLMs $p_{\theta}$ と評価対象の状態の集合 $S$ によってこの関数を定義することが出来、 $V(p_{\theta}, S)$ のようにあらわすことが出来ます。状態 $s$ に対して $V(p_{\theta}, S)(s)$ のように評価関数に入力することでその状態の評価値を返します。

評価値としては、たとえばある状態に対し1～10までの数値で表現する方法や、"良い"/"どちらとも言えない"/"悪い"といった分類を与える方法で定義することが出来ます。一方文章を生成するなどのタスクの場合は単純な値や分類で評価値を表現できないこともあります。その場合はどの状態がいいかを選択させる処理を複数回実行し、選択された回数、つまり投票された回数を評価値として表現することも出来ます。

探索アルゴリズムを定義する

思考ステップ生成関数と状態の評価関数を用いてToTの木構造から最適なプロセスを探索するためのアルゴリズムを定義する必要があります。常に決まった数の候補の状態を保持しながら探索を進めていくBreadth-first-search(BFS)というアルゴリズムと、今考えられる最適な状態を選択し続けていき、評価値が一定のしきい値を下回った場合は一つ前の思考ステップに戻って別の状態を探索するDepth-first-search(DFS)というアルゴリズムが論文では紹介されています。

BFSとDFSのアルゴリズムの流れについて、論文に掲載されている図を転載致します。

具体的なタスクにおけるToTの実装イメージ

具体的なタスクにおいてToTがどのように実装されるのかを見ていきます。論文では"Game of 24", "Creative writing", "Mini Crossswords"という3つのタスクにおけるToTの実装の方針が紹介されていました。今回はこのうちの"Game of 24"について調べてみました。

より具体的なPromptの内容を知るため、ToTのOfficial Repositoryである以下のGithub Repositoryを参照しました。

github.com

Game of 24

Game of 24は与えられた4つの数字と四則演算を組み合わせて結果が24になる計算式を求めるタスクです。このタスクをToTのフレームに落とし込むと次のようになります。

思考ステップ

たとえば4, 9, 10, 13という数字が与えられたとき、選択する思考ステップは、現在残っている数字の中から2つを選んで作ることが出来る4 + 9 = 13や13 - 10 = 3のような計算式で表現することが出来ます。

ステップ生成関数

論文内で $G(p_{\theta}, s, k)$ で表現されていた関数は、Propose PromptというPromptの形で実装することが出来ます。Official Repositoryの"src/tot/prompts/game24.py"にこのPromptが実装されており、その個所を以下に抜粋します。

'''Use numbers and basic arithmetic operations (+ - * /) to obtain 24.
Input: 4 4 6 8
Answer: (4 + 8) * (6 - 4) = 24
Input: 2 9 10 12
Answer: 2 * 12 * (10 - 9) = 24
Input: 4 9 10 13
Answer: (13 - 9) * (10 - 4) = 24
Input: 1 4 8 8
Answer: (8 / 4 + 1) * 8 = 24
Input: 5 5 5 9
Answer: 5 + 5 + 5 + 9 = 24
Input: {input}
'''

{input}に現時点で残っている数字が入力され、次に取るべきステップが生成される、という仕組みになっています。

評価関数

論文では $V(p_{\theta}, S)$ と表現されていた評価関数もValue PromptというPromptの形で実装することが出来ます。こちらもOfficial Repositoryの"src/tot/prompts/game24.py"に実装されており、その個所を以下に抜粋します。

'''Evaluate if given numbers can reach 24 (sure/likely/impossible)
10 14
10 + 14 = 24
sure
11 12
11 + 12 = 23
12 - 11 = 1
11 * 12 = 132
11 / 12 = 0.91
impossible
4 4 10
4 + 4 + 10 = 8 + 10 = 18
4 * 10 - 4 = 40 - 4 = 36
(10 - 4) * 4 = 6 * 4 = 24
sure
4 9 11
9 + 11 + 4 = 20 + 4 = 24
sure
5 7 8
5 + 7 + 8 = 12 + 8 = 20
(8 - 5) * 7 = 3 * 7 = 21
I cannot obtain 24 now, but numbers are within a reasonable range
likely
5 6 6
5 + 6 + 6 = 17
(6 - 5) * 6 = 1 * 6 = 6
I cannot obtain 24 now, but numbers are within a reasonable range
likely
10 10 11
10 + 10 + 11 = 31
(11 - 10) * 10 = 10
10 10 10 are all too big
impossible
1 3 3
1 * 3 * 3 = 9
(1 + 3) * 3 = 12
1 3 3 are all too small
impossible
{input}
'''

ここでも{input}に現在残っている数字が入力され、結果として"sure", "likely", "impossible"のいずれかが得られます。"sure"は24に至るプロセスが明確に見つかった場合、"likely"は見つからないが24に近い値は計算できる場合、"impossible"は現在の数字では24に到底ならない(大きすぎる、または小さすぎる)場合です。

探索アルゴリズム

BFSを使用しています。常に5つの状態( $b=5$ )を保持しながら、それらを元に探索を進めていきます。

まとめ

今回はPrompt Engineeringのテクニックの一つ、Tree of Thoughts(ToT)について調べたことをまとめてみました。本当は実際に魔法陣の問題などを解いてみたいな・・・と考えていたのですが、今回は実装までは至りませんでした。ですので実装はまた次の宿題として取り組んでいきたいと思います。