DCGAN→WGAN-GPによってGANsの学習の安定化を実現しました。 - CCCMKホールディングス TECH LABの Tech Blog

こんにちは、技術開発ユニットの三浦です。

先日3Dプリンタが動くところを見せてもらったのですが、だんだんモノが出来ていく様子はずっと見ていても飽きないな、と感じました。これを見ながら一日過ごせそうだなぁと。ニューラルネットワークが学習を繰り返していくうちに、だんだんとそれっぽい画像を生成出来るようになっていく様子を見ているのも、それに通じるものがあります。

さて今回もGANsに関する話を紹介させていただきます。

まずは生成した「スパゲティボロネーゼ(ひき肉のスパゲティ)」の画像をご覧ください。

品質はまだあまりいいとは言えないものの、それらしい画像が生成出来るようになりました。さらに下のグラフのように、学習曲線がきれいに収束するようになり、学習がより安定するようになりました。

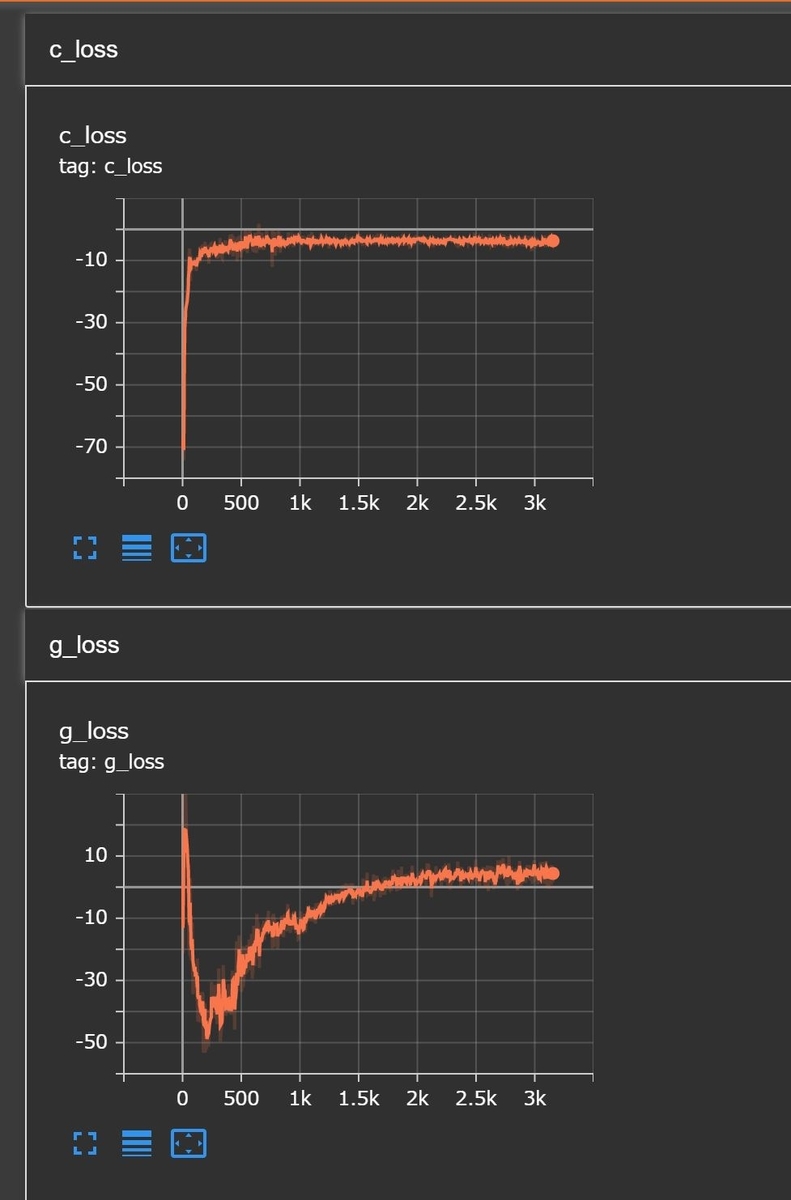
c_loss: discriminatorのloss/g_loss: generatorのloss

この改善を実現するために、「Wasserstein GANs：WGAN」というGANsの学習における改善方法について調べ、そこにさらに「Gradient penalty」という工夫を取り入れた「WGAN-GP」を実際にKerasで実装し、試してみました。

今回は「WGAN」と「WGAN-GP」が提案されている2つの論文を読んだ内容をまとめ、ご紹介したいと思います。

GANsの改善

GANsにおける課題は大きく2つあると考えています。

高品質な画像を生成する
ハイパーパラメータやデータに依存せずに安定した学習を実現する

「高品質な画像を生成する」課題に対するアプローチには、画像を生成する"generator"をより複雑な構造にするなどがあります。浅いネットワークよりもより深いネットワークのほうが、より多くの画像の特徴をその内部に保持出来ると考えられるからです。

一方でネットワークが複雑になると、重みの勾配が消えたり爆発するような問題が起こるようになり、学習が難しくなります。ネットワークの構造に依らず、安定して学習を行うためのアプローチが必要になります。

Wasserstein GANs：WGAN

「Wasserstein GANs：WGAN」は以下の論文で提案されている手法です。

Wasserstein GAN
Martin Arjovsky, Soumith Chintala, Léon Bottou
Submitted on 26 Jan 2017 (v1), last revised 6 Dec 2017 (this version, v3)
[1701.07875] Wasserstein GAN

リアル画像が生成される分布とgeneratorによって生成される画像の分布をどうやって近づけていくのか、という観点でGANsの問題が考察されています。

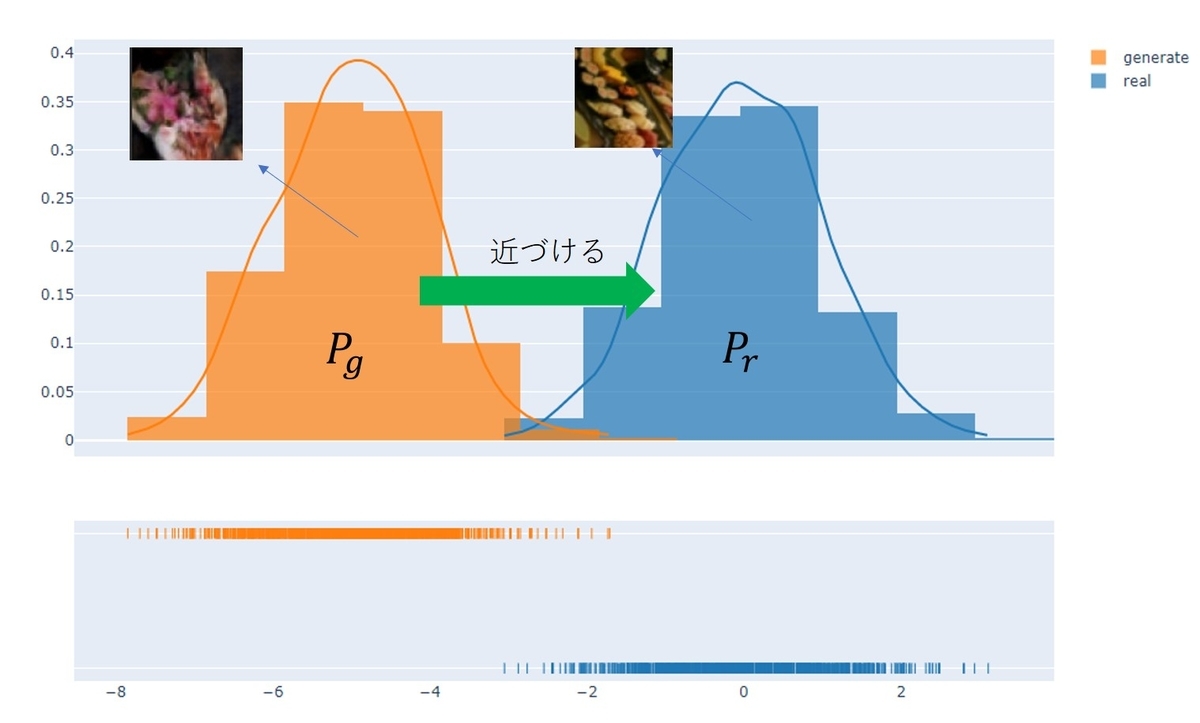
2つの分布を近づけるためには近さを測定するための適切な「距離」が必要で、その距離として「The Earth-Mover (EM) distance(Wasserstein-1)」をWGANでは採用しています。分布の近さを図る指標はたとえば「Kullback-Leibler (KL) divergence」や「Jensen-Shannon (JS) divergence」などがありますが、EM distanceはgeneratorを決定するパラメータ $\theta$ に対し連続になる条件が軽い、という特徴があります。

上記論文に取り上げられている例ですが、たとえば平面上で $(0, 0～1)$ に一様に分布する $P _ {0}$ と $(\theta,0～1)$ に一様に分布する $P _ {\theta}$ の2つの分布があったとき、EM distance( $W$ )とJS divergence( $JS$ )を計算すると以下のようになります。

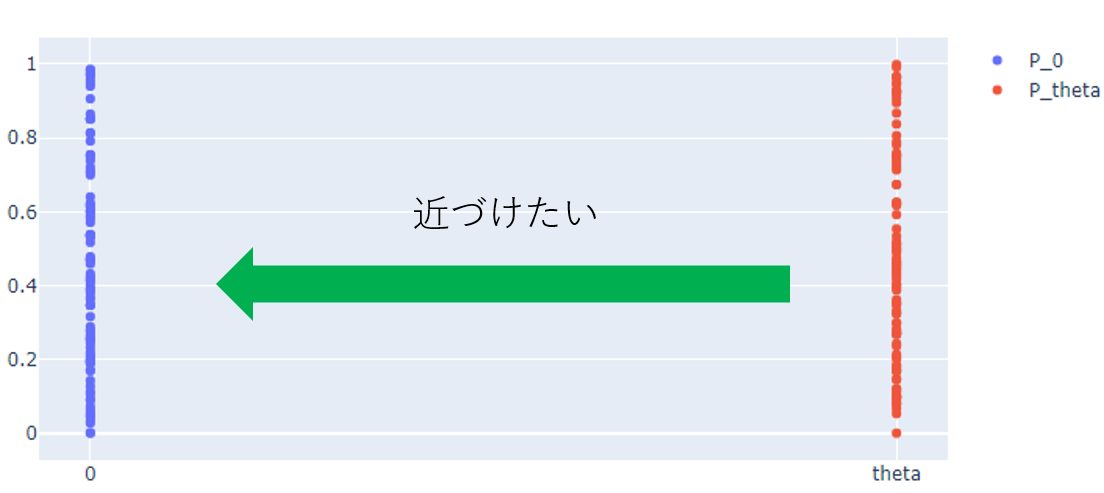
$W(\mathbb{P}_{0}, \mathbb{P}_{\theta}) = |\theta|,\\ JS(\mathbb{P}_{0}, \mathbb{P}_{\theta}) = \left\{ \begin{matrix}\log2&\mathbf{if}\quad\theta \not ={0}\\ 0&\mathbf{if}\quad\theta ={0} \end{matrix} \right.$

$\theta$ を0に近づけると2つの分布は明らかに近づいていきます。なのでその距離は徐々に0に近づいていって欲しいのですが、これを表現しているのはこの例ではEM distanceだけです(JS divergenceは $\theta=0$ 以外ではつねに $\log2$ で変化しない)。簡単な例ですが、EM distanceがより適していることが分かります。

このEM distanceは以下の計算式で求めることが出来ます。

$W(\mathbb{P} _ {r}, \mathbb{P} _ {\theta}) = \mathbf{sup} _ {\|f\| _ {L \leq 1}}\mathbb{E} _ {x \sim \mathbb{P} _ {r}}[f(x)] - \mathbb{E} _ {x \sim \mathbb{P} _ {\theta}}[f(x)]$

$\mathbf{sup} _ {|f| _ {L \leq 1}}$ は1-リプシッツ関数における上限を表しています。上限を与える $f$ を求めることは不可能な場合が多く、実際は $f$ を重み $w$ を持つニューラルネットワーク $f _ {w}$ で表現して、 $f _ {w}$ にリプシッツ連続であるという制限を課したうえで以下の最大化問題を解くことになります。

$\max _ {w\in\mathcal{W}}\mathbb{E} _ {x \sim \mathbb{P} _ {r}}[f _ {w}(x)] - \mathbb{E} _ {x \sim \mathbb{P} _ {\theta}}[f _ {w}(x)]$

実際にプログラムで解く場合は、この式の符号を反転して損失関数とし、最小化問題として解きます。 $W(\mathbb{P} _ {r}, \mathbb{P} _ {\theta})$ の近似解が求まったら、 $\theta$ を $W(\mathbb{P} _ {r}, \mathbb{P} _ {\theta})$ が減少する方向に動かすことで $\mathbb{P} _ {\theta}$ を $\mathbb{P}_{r}$ に近づけていくことが出来ます。

WGANではこのような手続きでgeneratorが生成する画像の分布をリアル画像の分布に近づけていき、よりリアルな画像を生成出来るようにします。

この論文を読んで感じたのですが、DCGANではdiscriminatorとgeneratorが勝負をすることでネットワーク全体を学習させる、という印象を持っていたのですが、WGANはどちらかというとdiscriminatorとgeneratorが協力し合ってネットワーク全体を学習させるという印象を持ちました。WGANの論文においてはdiscriminatorのことをcritic(評論家)という言葉で表しています。

WGAN-GP

先のWGANの最大化問題において、 $f$ が1-リプシッツ連続であるという制限が必要になるのですが、これをどう表現するのか、という問題があります。 $f$ が1-リプシッツ連続であるとは、それが定義されている $X$ 上のどんな2点 $x_1, x_2$ に対しても以下が成り立つことです。

$|f(x_1) - f(x_2)| \leq |x_1 - x_2|$

つまり、傾きの絶対値が1以下であるという制限が課せられます。

WGANの論文では、これを実現するために、 $f _ {w}$ の重み $w$ の取りうる値の範囲をコンパクトな空間、具体的にはある定数 $c$ を取って $w$ の要素の値が $[-c, c$ ] の範囲に収まるようにしています。これは、 $w$ が動く空間 $\mathcal{W}$ がコンパクトなら、 $c$ と $f$ のネットワーク構造によって決まる定数 $K$ が存在し、 $f _ w$ は $K$ -リプシッツ連続になる、という性質を利用しているようです。プログラム上では重みの更新時にこの範囲に収まるように適宜クリッピングをかけています。

ただこの方法だと勾配の消滅や爆発が起こることがあるようで、その改善案として提案されたのが「Gradient penalty」を $W(\mathbb{P} _ {r}, \mathbb{P} _ {\theta})$ の近似解を求めるときに課す、という方法です。

こちらは以下の論文で提案されています。

Improved Training of Wasserstein GANs
Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron Courville
Submitted on 31 Mar 2017 (v1), last revised 25 Dec 2017 (this version, v3)
[1704.00028] Improved Training of Wasserstein GANs

先ほどの1-リプシッツ連続の定義より、 $f$ が1-リプシッツ連続であるためにはどの2点においても傾きの大きさ(ノルム)が1以下でなければなりません。これを満たすように、discriminatorの損失関数に「Gradient penalty」の項を追加します。

WGAN-GPにおいてdiscriminator側で最小化する損失関数は、「Gradient penalty」を含んだ以下の式になります。

$L = \mathbb{E} _ {\tilde{x} \sim \mathbb{P} _ {g}}[D(\tilde{x})] - \mathbb{E} _ {x \sim \mathbb{P} _ {r}}[D(x)] + \lambda \mathbb{E}_{\hat{x} \sim \mathbb{P}_{\hat{x}}}[(\|\nabla_{\hat{x}}D(\hat{x}) \|_{2} - 1)^{2}]$

一番後ろの項が「Gradient penalty」で、サンプリングした $\hat{x}$ における傾きの大きさが1よりも大きいとより大きなペナルティが損失関数に課されるようになっています。 $\lambda$ は「Gradient penalty」にかける重みで、論文では10.0という値が推奨されています。

その他の工夫

2つの論文で共通しているのが、discriminator(critic)の学習の回数を多く取っている点です。具体的には5回discriminatorをbatchで学習させた後、1回generatorをbatchで学習する、という方法を取っています。一番最初に掲載した学習曲線もそうなのですが、まずdiscriminatorの方を安定させてからgeneratorを学習していく、というのがGANsを安定して学習させるいい方法なのかもしれません。

また、オプティマイザーはWGANではRMSPropを、WGAN-GPではAdamを採用している、という違いがありました。