データアナリストの小林です。
当社では様々な媒体で、クライアント・アライアンス様の販売促進・CRMの支援をさせていただいております。

その中で、「マーケティング施策の効果検証」は欠かせないテーマの一つです。
当社がもつ7000万人のシングルID情報と実購買データによって、例えば介入・統制群を分けたRCT（ランダム化比較試験）やA/Bテストを実施し、介入効果の客観的な測定に努めています。

ところで、上記RCTやA/Bテストのような比較対象を用意できる施策であれば、効果検証は容易かと思いますが、定常的なマス広告や全店値下げキャンペーンなど、適切な比較対象を用意できない・前後比較ができないケースでは、その効果をどのように測ればよいでしょうか？

この記事では、上記課題に対する一つの解決策として、いわゆる回帰分析の延長である状態空間モデルを用いた介入効果測定の技法紹介とその限界を探ります。

状態空間モデル

観測できない隠れた状態を示す「状態モデル（システムモデル）」と、その状態に外部要因とノイズが加わって結果が表れる「観測モデル」であらわされる統計モデルです。特にその拡張性の高さから、時系列・空間データにて利用されることが多く、時系列モデルは以下のように表されます。

f:id:kopaprin:20210330172353p:plain

$\begin{aligned} \ \mu_{t} &= h(\mu_{t-1})+\nu_{t} &(1) \\ \ y_{t} &= f(\mu_{t})+\epsilon_{t} &(2) \end{aligned}$

(1)が状態を示す状態モデル、(2)が観測モデルの数式です。
この状態空間モデルを利用すると、以下のように時系列データにおける介入変数の効果を数式化できます。

$\begin{aligned} \ \mu_{t} &= h(\mu_{t-1})+\nu_{t} \\ \ y_{t} &= f(\mu_{t})+\alpha * X_{t}+\epsilon_{t} \end{aligned}$

つまり、状態モデル $\mu$ を何も介入をしなかった反実仮想の状態ととらえ、
それに介入変数 $X$ とその効果 $\alpha$ が加わり、 $t$ 時点の結果が観測されていると捉えます。

例えば、目的変数 $Y$ を売上とし、チラシ発行１部あたりの売上向上効果が 100 円だった場合、 $X$ はチラシ発行部数、 $\alpha$ は 100 になり、チラシ発行部数 × 100 円が介入効果として $\mu$ に加わり、 $Y$ が観測されるモデルになります。

ベイズモデルの利用

状態空間モデルを実装するにあたり、よく利用されるのがMCMC(マルコフ連鎖モンテカルロ法)サンプリングを利用してパラメータ推定を行うベイズモデリングです。
状態空間モデルはその柔軟性ゆえ、最尤法によるパラメータ推定が困難になりえます。
そこで、乱数サンプリングアルゴリズムによりパラメータの事後分布を疑似的に作り出すのがMCMCによるベイズモデリングのアイデアです。

パラメータの分布を作り出せるという点が効果検証結果の顧客説明にも役立ち、「95%の確率で介入効果はxx～xxの範囲にあるといえます。」と言うことが可能です。
（頻度論に基づく最尤法ではパラメータを定数として考えるため、この言い方ができません）

状態空間モデル・ベイズモデルはすでに様々な書籍・文献・WEBで詳しい内容が公開されているので、適宜ご参照いただくとよいと思います。

シミュレーション

では、状態空間モデル・ベイズモデルで、介入効果を推定できるのかシミュレーションを行います。

# 実装はgooglecolabを利用
# 可視化内容など、本筋と無関係なコードは部分的に省略しています。
import pandas as pd
import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
import seaborn as sns
import statsmodels.api as sm
import pystan
import arviz

np.random.seed(seed=123)

以下のとおり、時系列データと介入効果・介入変数を生成します。

T = np.arange(0,100)
sin = np.sin(np.linspace(0, 30, 100))*10 + 100
trend = 0.3*T
sigma = np.random.normal(0,1,(100))

x1 = np.random.rand(100)
x2 = np.random.rand(100)
y = trend + sin + sigma + 10*x1

生成した介入前データと介入後データ、自己相関(Autocorrelation)は以下のような状況です。

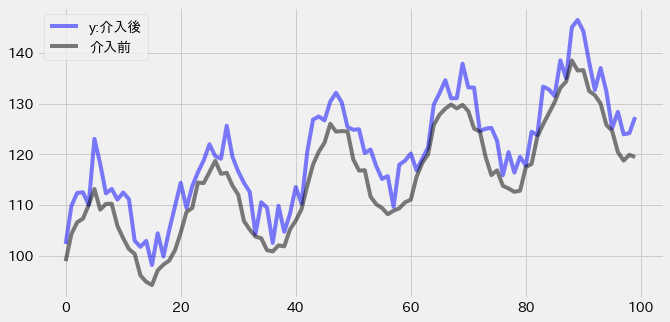
f:id:kopaprin:20210327001643p:plain

f:id:kopaprin:20210327150152p:plain

yはトレンド項trendと周期性sin、ノイズsigmaに、介入変数x1とその効果10を乗じた値を加算して生成しています。
sin波のベースと、単調な増加トレンド、固定の介入効果で生成された目的変数であるため、かなりシンプルなデータとなっています。
まずはこのデータで、x1のパラメータ（介入効果10）が推定できるかどうかがテーマです。
さらに、今回のモデルでは、まったくyに影響を与えない変数x2も組み込みました。 x1の真のパラメータ10と、x2のパラメータ0(理論上は何も影響与えていないため)を正しく推定できるかどうかテストします。

効果を測定するモデル式は以下のとおりです。

$\begin{aligned} \ \mu[t] &\sim Normal(2\mu[t-1] - \mu[t-2] , \sigma_{\mu} ) \\ \ season[t] & \sim Normal(-\Sigma_{l=1}^{L-1}season[t-l], \sigma_{season}) \\ \ y\_mean[t] &= \mu[t] + season[t] \\ \ Y[t] & \sim Normal(y\_mean[t] + a * x1[t] + b * x2[t], \sigma_{Y}) \\ \end{aligned}$

周期性seasonはAutocorrelationの結果から $L=20$ とします。

このモデルをstanを利用して実装します。
stanはベイズモデリングの実装で、大変有名なプログラミング言語です。
詳細は公式やその他解説ブログ等をご参照ください。

model = """
data{
  int T;
  vector[T] Y;
  vector[T] x1;
  vector[T] x2;
}
parameters{
  vector[T] mu;
  vector[T] season;
  real a;
  real b;
  real<lower=0> s_mu;
  real<lower=0> s_season;
  real<lower=0> s_Y;
}
transformed parameters{
  vector[T] y_mean;
  y_mean = mu + season; //状態モデル

}
model{
  mu[3:T] ~ normal(2*mu[2:(T-1)]-mu[1:(T-2)],s_mu); //2階差分トレンド
  for (t in 20:T)
    season[t] ~ normal(-sum(season[(t-19):(t-1)]),s_season);  //Autocorrelationに基づく周期性（20間隔）
  Y ~ normal(y_mean + a * x1 + b*x2, s_Y); //観測モデル
}
"""

st_model = pystan.StanModel(model_code=model)

data = {
    "T":len(T),
    "Y":y,
    "x1":x1,
    "x2":x2
}

fit_model = st_model.sampling(data=data,iter=2000,chains=4,warmup=1000,algorithm="NUTS",n_jobs=-1,verbose=True,seed=123)

fit_modelの収束判定指標Rhatが1.1を下回り、各パラメータのトレースプロットが安定するのが目安です。

f:id:kopaprin:20210329112344p:plain

まずはx1のパラメータaと、x2のパラメータbの分布をみてみます。

f:id:kopaprin:20210327010015p:plain

上記のとおり、x1のパラメータEAP推定量（期待値）は 9.62 で、真の値 10 に近い値を推定できています。
また、x2のパラメータも -0.64 と、真の値 0 に近い値となっています。

実測値yと介入前の状態（trend + sin + sigma）、システムモデル予測値y_meanをプロットすると以下のような状況です。

f:id:kopaprin:20210327005924p:plain

システムモデル予測値は、介入前状態に近い値を推定できていることがわかります。
それに伴い、介入影響も真値に近い値を推定できているようです。

売上データでの適用

先程のデータはトレンド・周期性成分ともに非常に単調な内容であったため、真値に近い推定結果だった可能性が考えられます。
そこで、実際の売上データで介入効果を仮定した場合でも推定可能か検証します。
売上データには、kaggleデータセットを用いることにします。

www.kaggle.com

DatasetのOverviewによれば、これはロシア最大のソフトウェア会社の1つである1C Companyから提供された、商品の販売データとのことです。

df = pd.read_csv("/sales_train.csv")
df["sales"] = df["item_price"]*df["item_cnt_day"]
df["date"] = pd.to_datetime(df["date"].str.strip(),format="%d.%m.%Y")
df = df.groupby("date").agg({"sales":"sum"})
df = df[(df.index>=datetime(2013, 2, 1))&(df.index<datetime(2013, 5, 1))]
df["sales"] = (df["sales"]/10000).astype(int)

検証用として、２ヶ月間の総売上を抽出します。
なお、売上はわかりやすく単位を変換しています。
データを以下に示します。

f:id:kopaprin:20210327154955p:plain

f:id:kopaprin:20210327201401p:plain

不定期変動がありそうですが、周期性はきれいな７日周期となっており、日別売上データで一般的な傾向かと思います。

さきほどと同様に、このデータに意図的に介入変数x1と介入効果10を加えます。無関係な変数x2も同様です。

sales_df["x1"] = np.random.gamma(2,100,len(sales_df))
sales_df["x2"] = np.random.gamma(2,100,len(sales_df))
sales_df["y"] = sales_df["sales"] + sales_df["x1"]*10

擬似的に作り出した介入効果により、売上実数に下駄を履かせた結果が以下のとおりです。 f:id:kopaprin:20210327203104p:plain

stanのコードはさきほどのモデルの周期性のみ $L=7$ に変更し、同じようにMCMCサンプリングを行います。

model = """
data{
  int T;
  vector[T] Y;
  vector[T] x1;
  vector[T] x2;
}
parameters{
  vector<lower=0>[T] mu;
  vector[T] season;
  real a;
  real b;
  real<lower=0> s_mu;
  real<lower=0> s_season;
  real<lower=0> s_Y;
}
transformed parameters{
  vector[T] y_mean;
  y_mean = mu + season;

}
model{
  mu[3:T] ~ normal(2*mu[2:(T-1)]-mu[1:(T-2)],s_mu);
  for (t in 7:T)
    season[t] ~ normal(-sum(season[(t-6):(t-1)]),s_season);
  Y ~ normal(y_mean + a * x1 + b*x2, s_Y);
}
"""

st_model = pystan.StanModel(model_code=model)

data = {
    "T":len(df),
    "Y":df["y"],
    "x1":df["x1"],
    "x2":df["x2"]
}

fit_model = st_model.sampling(data=data,iter=4000,chains=4,warmup=2000,algorithm="NUTS",n_jobs=-1,verbose=True,seed=123)

サンプリングしたパラメータの分布を見てみます。

f:id:kopaprin:20210327211021p:plain

x1のパラメータは10.27で、真の値10に近い値となっており、
x2のパラメータも真の値0に近い-0.47となっています。

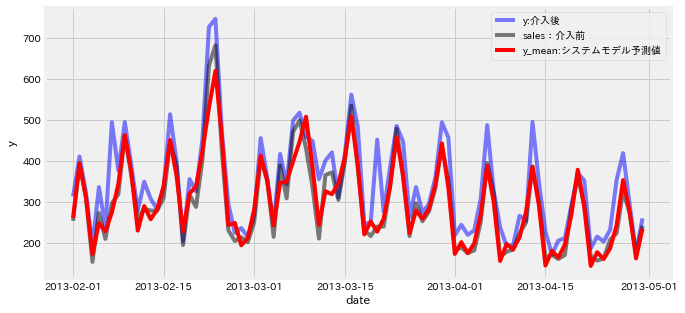
f:id:kopaprin:20210330212724p:plain

先ほどと同様に、介入効果を除いた状態（元データのsales）をよく推定できていることも分かります。

単調なsin派と増加トレンドではない時系列データでも、介入効果を推定することができました。

モデルの限界点と可能性

ここまで、ベイズ状態空間モデルにより介入効果を真値に近い値で推定できている例を示してきました。
ただし、現実問題ではここまで単純に効果を測定できない場合がほとんどだと思います。

介入効果のキャリーオーバー効果
　例えばある１日にCMを流した場合、その効果はその日だけでなく数日間続くことが容易に想定できます。今回のように1日だけの介入量だけで効果を検討するのは不適当です。
介入効果の収穫逓減
　広告効果は最初の投下が最も効果が高く、続けるに従い単位あたりの効果量が減り、限界に近づいていくと言われています。これを収穫逓減の法則と言いますが、この効果も加味していません。
介入効果の季節・エリア・個別変動要因
　介入効果は常に一定ではありません。介入する時期や内容、エリア、競合の動向や景気等に大きく左右されることは容易に想定できます。

上記のような理由から、単調なモデルはあまり効果的ではない可能性があります。
かなり難しい背景を仮定することが必要そうですが、MCMCサンプリングによるベイズモデリングであれば柔軟にモデルを設計できるため、上記のような問題に対処する手法も研究されています。
Bayesian Methods for Media Mix Modeling with Carryover and Shape Effects

以上、理論的には状態空間モデル（回帰モデル）のパラメータによって介入効果が測定できること、
複雑な仮定が必要な広告効果でも、ベイズモデルによりモデル化・対処できることを学ぶことができました。

ただし、介入効果を正確かつ簡単に測定できるのはRCT、A/Bテストを始めとした対照群との比較実験です。
ここで紹介したモデルはあくまで「やむを得ない」効果測定方法であると捉え、可能な限り小規模でも比較実験を取り入れることが肝要であると思いました。

--参考--

StanとRでベイズ統計モデリング / 松浦健太郎著石田基広監修市川太祐高橋康介高柳慎一福島真太朗松浦健太郎編集 | 共立出版

効果検証入門～正しい比較のための因果推論／計量経済学の基礎：書籍案内｜技術評論社

Marketing Mix Modelling Step-by-Step — Part 1: Building the Model | by Morten Hegewald | The Startup | Medium