LLMの性能を測る指標をベンチマーク結果から取得する方法について、論文を読みました。

こんにちは、CCCMKホールディングス TECH LABの三浦です。

昨年参加したAI・機械学習カンファレンス"NeurIPS2024"のポスターセッションで発表されていた論文の中で、面白いアプローチだな、と印象に残っている論文がいくつかあります。

そのうちの1つがこちらの論文です。

Title: Observational Scaling Laws and the Predictability of Language Model Performance
Author: Yangjun Ruan, Chris J. Maddison, Tatsunori Hashimoto
Submit: 17 May 2024 (v1), last revised 1 Oct 2024
arXiv: https://arxiv.org/abs/2405.10938

今回の記事では、最初にこの論文で紹介されている手法についてまとめ、その後に日本語でのベンチマークを用いて論文と同様の結果が得られるのを確認してみました。

論文の提案手法について
- Scaling laws
- FLOPsに代替するモデル性能指標
日本語ベンチマークでのPCA
まとめ

論文の提案手法について

Scaling laws

Transformerを構造に持つLLMでは、"Scaling laws"と呼ばれる特性が見られることが広く知られています。Scaling lawsは事前学習時の学習量(FLOPs)、モデルのパラメータ数、学習データサイズとモデルの性能の関係性を表しており、それぞれの変数の値が増加するほどモデルの性能が向上する関係があります。

関係性は分かっているものの、FLOPsが増加するとどれだけ性能が向上するのかについては、実際にいくつかのモデルを学習し、その結果を用いて推計をする必要があるため、Scaling lawsを求めることはかなり負荷が高い作業になります。

また、現在様々なLLMが誕生し、それぞれのLLMは独自の学習の工夫がなされています。それらの学習の工夫によってScaling lawsがどのように変化するのか(たとえば同じFLOPsの増加でより性能が向上する学習手法の方がより効率的と考えられます)といった考察は、各モデルの学習時のFLOPsを把握する必要があるのですが、実際にそれらを知るのは困難です。

FLOPsに代替するモデル性能指標

学習時のFLOPsとモデルの性能には関係性があるが、その関係性を推計することが困難である、という問題に対し、FLOPsと相関がある性能指標を公開されているLLMのベンチマーク結果から取得する、というアプローチを論文では取っています。

たとえばHugging Faceでは"OpenLLM Leaderboard"という、オープンソースのLLMに対して複数のベンチマークによる性能結果の一覧表を公開しています。

huggingface.co

論文の提案手法では、モデルxベンチマークの行列に対し、主成分分析(PCA)を実行します。

Observational Scaling Laws and the Predictability of Language Model Performance, Figure 1

するとデータのばらつきの80%を第一主成分で、第一～第三主成分で96.7%を説明出来ていることが確認されています。各主成分ベクトルの要素を見ると、第一主成分は全てのベンチマークに関係するLLMの一般能力、第二主成分は推論、第三主成分はプログラミング能力に関連している、という結果が紹介されています。

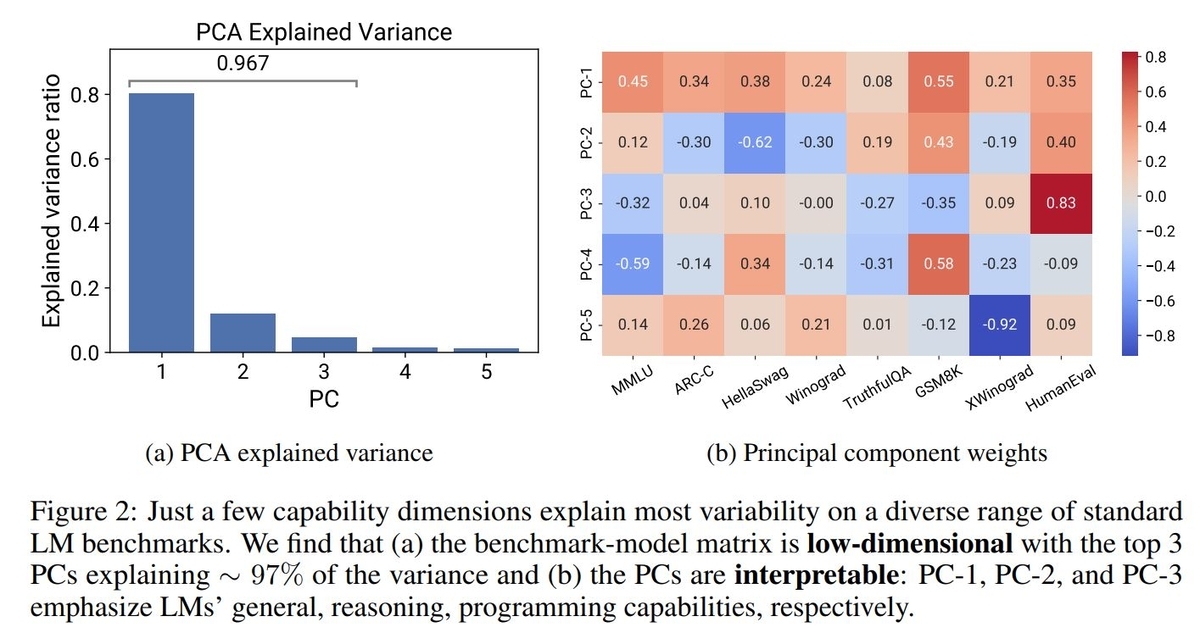
Observational Scaling Laws and the Predictability of Language Model Performance, Figure 2

さらに各LLMの第一主成分のスコア(PC1)とFLOPsの間には対数線形の関係が確認されています。上位の主成分スコアを用いてFLOPs(の対数)の近似値を計算することで、Scaling lawsの近似計算が可能になります。

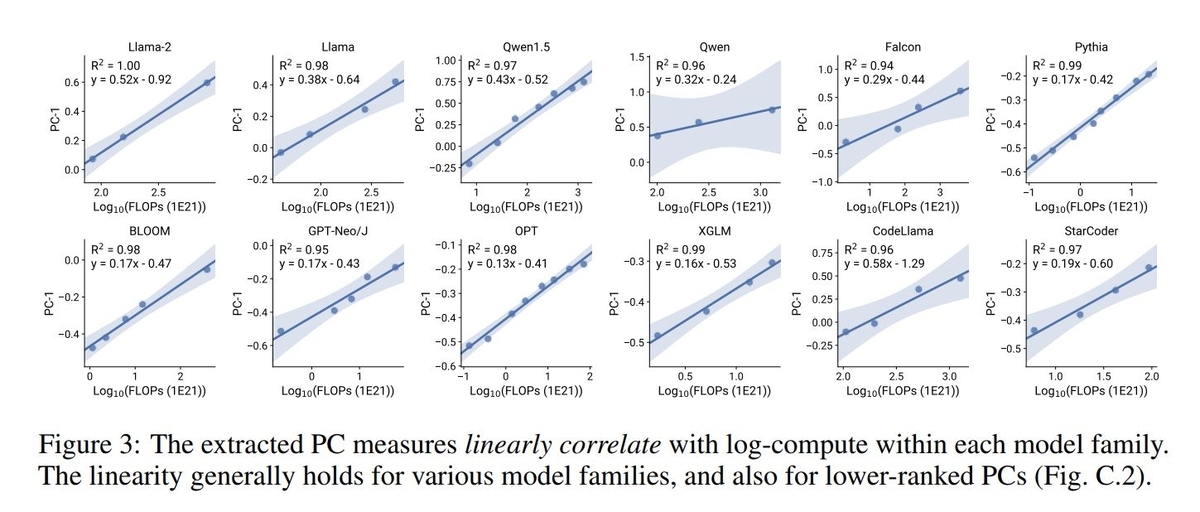
Observational Scaling Laws and the Predictability of Language Model Performance, Figure 3

日本語ベンチマークでのPCA

論文におけるベンチマーク結果に対するPCAの適用、というアプローチがとても面白く、印象に残りました。たとえば同じアプローチを日本語のベンチマーク結果に対して適用したら同じような結果が出てくるのか、確認してみたいと考えました。

オープン・クローズLLMに対し、日本語データセットを使った多用なベンチマーク結果をWeight&Biases様が"Nejumi LLMリーダーボード3"として公開されています。

wandb.ai

このデータにPCAを実行し、どのような結果が得られるかを検証してみました。

作成したプログラム

最初にNejumi LLMリーダーボード3の総合評価をCSVでエクスポートしました。今回は測定結果のうち汎用的言語性能 (General Language Processing, GLP)に該当するものを対象にしました。PCAの実行はscikit-learnを使用しました。

PCAの実行までのコードです。

import pandas as pd
from sklearn.decomposition import PCA

bench_mark = pd.read_csv(
    "wandb_export_....csv"
)

models = bench_mark["model_name"]
pca_target_columns = [c for c in bench_mark.columns if c.startswith("GLP_")]
pca_dataset = bench_mark[pca_target_columns]

pca = PCA()
pca.fit(pca_dataset)

各成分による説明率

まず各主成分の寄与率を確認してみました。

import pandas as pd
import plotly.express as px

explained_variance = pd.DataFrame(
    pca.explained_variance_ratio_,
    columns=["Explained Variance"]
)
explained_variance["PCs"] = [f"PC{i+1}" for i in range(len(explained_variance))]
fig = px.bar(explained_variance, x='PCs', y='Explained Variance')
fig.show()

結果はこのようになりました。

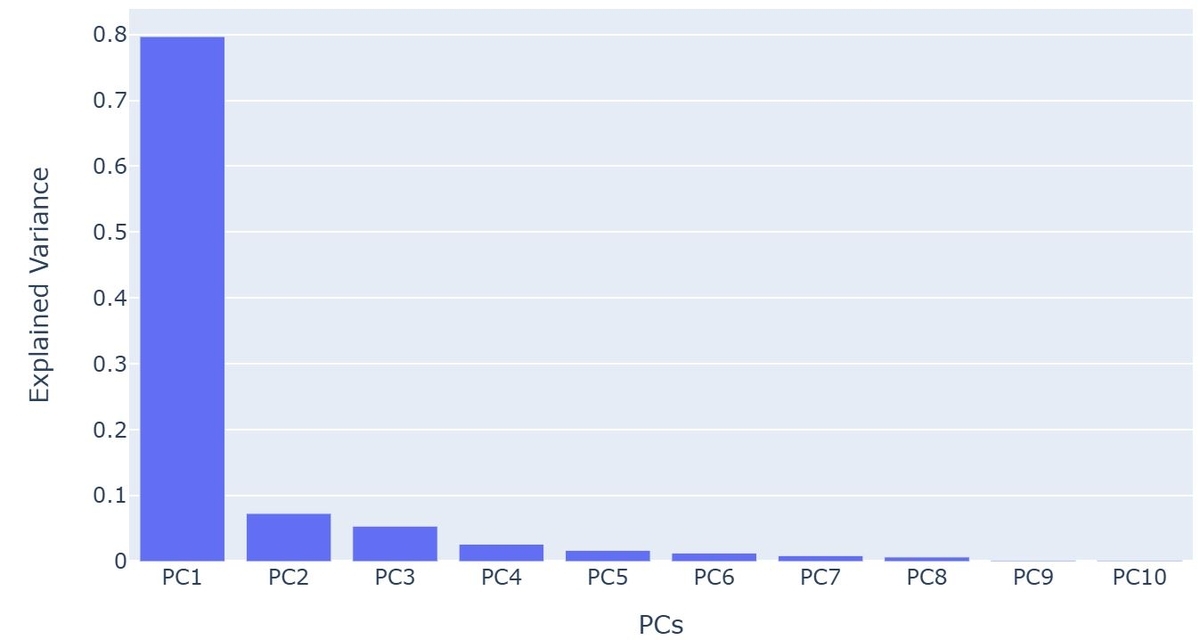
第一主成分で全体の約80%を説明し、第三主成分までで90%程度説明出来ている、という結果になりました。

主成分ベクトルの表示

次に主成分ベクトルの成分を表示してみます。実行したコードは以下です。

import plotly.express as px

components = pd.DataFrame(
    pca.components_, 
    columns=pca_target_columns
)
px.imshow(components, text_auto=True)

結果はこちらです。

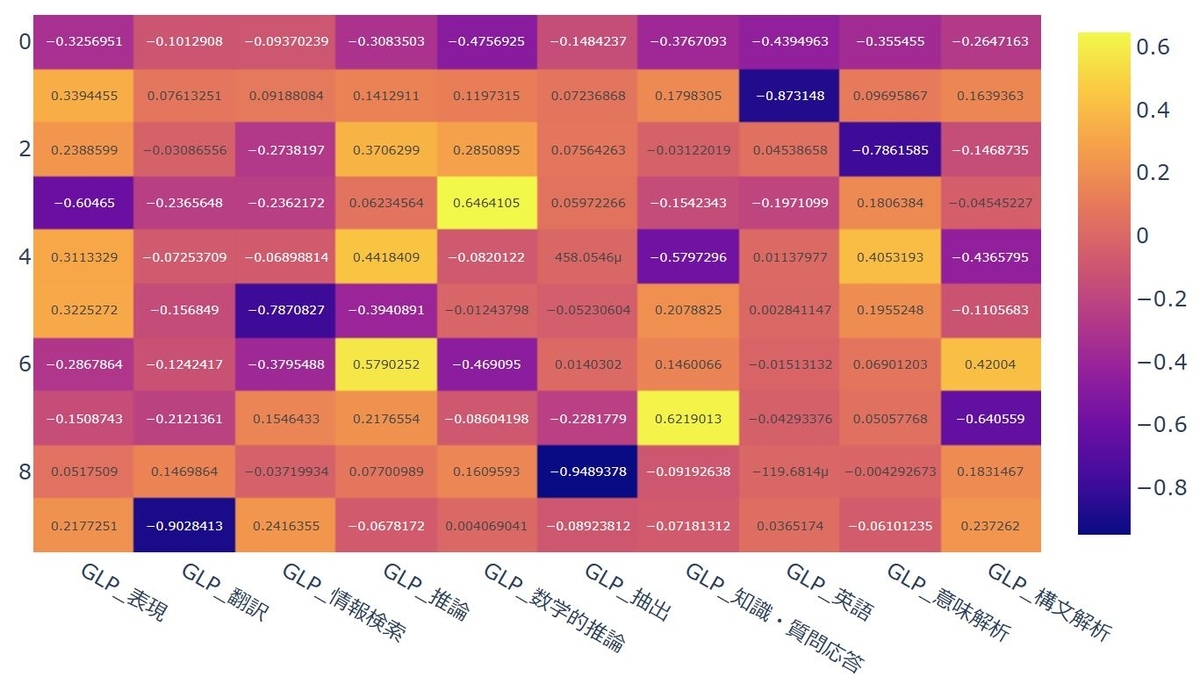
値がマイナスになってしまったのですが、第一主成分は全ての要素が同じ向きを示していることから汎用的な能力を表していると考えられそうです。第二主成分は英語能力、第三主成分は意味解析に関係があると言えそうです。

まとめ

今回はLLMのベンチマークの結果からLLMの性能指標を抽出し、それがScaling lawsの変数である学習時のFLOPsと相関があることを提示した論文を参考に、Weight&Biases様が公開している"Nejumi LLMリーダーボード3"の結果に対して同じようなアプローチを行い、日本語リーダーボードでも同じような傾向がありそう、ということを確認するところまで試してみました。

論文では提案手法によって得られた性能指標を用いて様々な考察がされており、もう少しじっくりと読み解いていきたいと思っています。